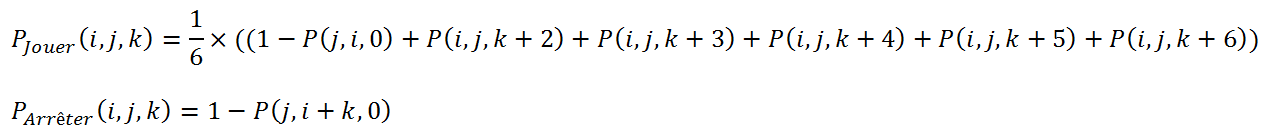« Vouloir gagner, c’est accepter de ne pas être bon ». Voilà comment aurait pu s’appeler ce billet si je n’avais pas peur du feu et des coups de fourches. Mais avant de laisser votre liberté d’objection répondre à ma liberté de provocation, et puisque les fourches sont sorties, voyons ensemble un petit cas pratique : le jeu des cochons.
Que ce soit, sportivement, socialement ou même financièrement, la société nous a toujours poussés à appréhender la performance derrière le prisme de la compétition et du record. D’ailleurs « Etre bon » n’est-il pas devenu aujourd’hui une façon euphémique de signifier que l’on n’est pas le meilleur ?
Tenter de se vaincre mutuellement, le cercle vertueux semble pourtant bien établi.
Toutefois, il arrive des jours comme aujourd’hui où je me rappelle soudain que gagner ne signifie pas toujours performer. Paradoxalement, et n’en déplaise aux convaincus, « gagner » et « être bon » ne sont pas équivalents, et ces deux notions peuvent parfois différer significativement.
Une fois ceci acquis, rappelez-vous qu’il est toujours vital de se souvenir de ce à quoi l’on aspire… car la stratégie à suivre ne sera pas la même.

Introduction au jeu des cochons

En bref, le jeu des cochons est un jeu de dé très simple opposant deux joueurs. Lorsque son tour vient, un joueur a le droit de lancer le dé autant de fois qu’il le veut tant qu’il ne fait pas de « 1 ». Si l’obtient un « 1 », le joueur ne marque aucun point et cède son tour à l’adversaire. Toutefois avant chaque lancer de dé, le joueur possède deux options :
(i)     S’arrêter là et céder son tour à l’adversaire. Il marque alors les points cumulés sur tous les lancés de dé du tour.
(ii)   Relancer le dé et venir augmenter son capital de points sur le tour, sachant que s’il obtient « un 1 », il perdra l’ensemble des points cumulés sur le tour et devra céder son tour.
Le premier joueur à atteindre 100 points a gagné.
Ainsi, par sa structure, le jeu pourrait être comparé à une opération de spéculation sur des actifs financiers. Je risque un capital précédemment acquis pour tenter d’augmenter mon gain.

La performance: maximiser ses gains

Une stratégie cherchant à maximiser ses gains à chaque tour (ie minimiser le nombre de coups nécessaires pour atteindre 100) s’appuiera sur l’espérance mathématique de gain. En d’autres termes, compte tenu des probabilités d’occurrence de chaque nombre, quel montant suis-je en droit d’espérer à chaque tour ?  Là-dessus, les mathématiques peuvent nous aider, l’espérance de gain à chaque tour est de 20 points.

Explication : les nombres pouvant me permettre d’augmenter mon capital de points sont 2,3,4,5 et 6 (soit une espérance de gain de 4). Or, à chaque lancé de dé, je dispose d’une chance contre 5 de faire un « 1 » et ainsi de perdre. L’espérance totale d’un tour est donc de 5 x 4 = 20.

Ma stratégie consistera donc à viser les 20 points sur chaque tour et m’arrêter une fois ceux-ci obtenus.
Notons bien que cette stratégie ne s’inscrit pas dans un objectif de record (qui ne serait alors qu’une compétition contre moi même).
Cette stratégie me garantit juste d’ »être bon ».

Stratégie optimale pour la victoire

Maintenant, changeons un peu d’objectif, je ne cherche plus à maximiser mes gains à chaque tour (ce que j’ai appelé « être bon ») mais je cherche à battre mon adversaire.
Et bien là, croyez-le ou pas, la stratégie change complètement. En outre, le choix à opérer ne dépend plus de mon seul capital de points déjà acquis sur le tour, mais dépend également de mon total de points et du total de points déjà acquis de mon adversaire.
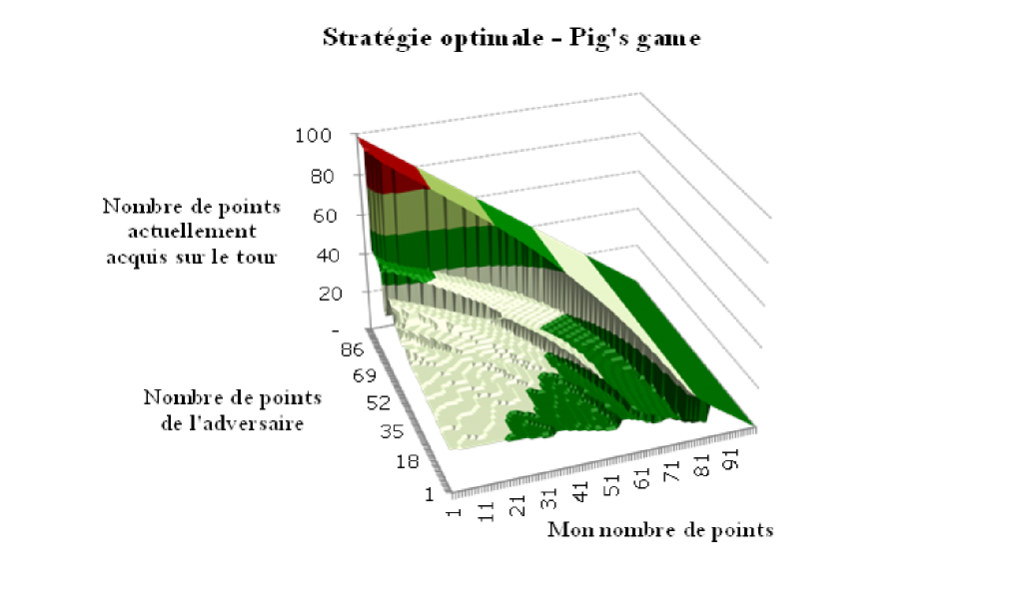
Ci-dessous, une vision en trois dimensions de la limite entre l’espace de décision « jouer » et l’espace de décision « s’arrêter là » d’après la stratégie optimale. On y représente ainsi le nombre de points k à atteindre sur un tour avant de s’arrêter en fonction du nombre de points i que je possède déjà et du nombre de points j de mon adversaire. Cette courbe a été obtenue sur Excel à partir du système d’équations décrit dans le chapitre ‘pour aller plus loin’.

Pour faire simple, si vous vous situez sous la surface, la stratégie optimale vous recommande de jouer, si vous êtes au–dessus, la stratégie optimale vous recommande d’arrêter, de comptabiliser vos points et de céder votre tour.
Prenons comme convention: i: mon nombre de points, j: le nombre de points de mon adversaire, et k: le nombre de points cumulés sur le tour auquel il m’est recommandé de m’arrêter de jouer.
Assez logiquement, la surface de décision est bornée par le plan k=100-i. En effet, si mon nombre de points est de i=70 et que mon score cumulé sur le tour est de k=30, je n’ai aucune raison de continuer à jouer, j’ai gagné et ce quelque soit le nombre de points j de mon adversaire.

Comparaison des deux stratégies

A priori, les deux objectifs ne semblait pas si différents l’un de l’autre. D’un côté je cherchais à maximiser mon score à chaque tour et de l’autre je cherchais à battre mon adversaire. Intuitivement, on pouvait quand même prévoir quelques dissemblances aux cas limites. Exemple: je suis à 78 points, mon adversaire est à 95 points, je ne vais pas m’arrêter à 20 points et lui laisser le dé alors que je suis à deux points de la victoire.
Toutefois, on aurait pu se dire que, à une vache près, les cas doivent se compenser. On aurait même pu penser que la surface de la courbe (représentant le nombre de points pour lequel il faut arrêter de jouer et céder son tour) avait pour moyenne 20. N’y pensez pas, la moyenne est de 26 coups dans la seconde stratégie, soit 30% de plus que l’espérance mathématique de gains!

Ainsi, en moyenne, la stratégie 2, en intégrant le facteur ‘adversaire’, nous incite à jouer là où la stratégie 1 et le calcul de l’espérance mathématique nous recommande d’arrêter.

Pour ma part, j’aime à dire que cet écart traduit le coût de la ‘prise de risque’ induite par la compétition.
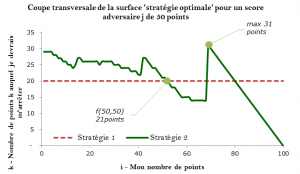
Enfin, seul point de rapprochement entre les deux stratégies, lorsque je me place loin des limites de la deuxième stratégie, c’est à dire dans le cas où mon adversaire et moi-même comptabilisons tous deux 50 points, dans ce cas le k optimal est à 21 points. Ainsi dans cette situation ponctuelle, les deux stratégies se rejoignent (cf ci-dessous – coupe transversale obtenue pour un nombre de points de l’adversaire fixé à 50 points).

Ci-dessus, sont représentés les deux stratégies dans le cas spécifique où mon adversaire a 50 points au compteur. La stratégie 1, qui ne tient pas compte de la compétition avec mon adversaire, prévoit comme décrit plus haut un k fixe à 20 points et intersecte la stratégie 2 quand mon nombre de points avoisine 50 points.

Conclusion 

La stratégie pour gagner est différente de la stratégie visant à maximiser le nombre de points à chaque tour.
Une fois cette réalité acceptée et digérée, peut-être pourriez-vous vous réinterroger sur vos vrais intentions au quotidien.
Voulez-vous être le plus heureux possible ou plus heureux que votre voisin ? Voulez-vous maximiser les gains de l’entreprise ou dépasser les résultats obtenus l’an passé ?Vous pensiez sans doute que ces objectifs accouchaient des mêmes stratégies, aujourd’hui vous savez que c’est faux, alors réfléchissez une fois encore sur le cap, il se pourrait bien que l’itinéraire change un peu.

Références:
Todd W. Neller and Clifton G.M. Presser. Pigtail: A Pig Addendum, The UMAP Journal 26(4) (2005), pp. 443–458.
Todd W. Neller and Clifton G.M. Presser. Practical Play of the Dice Game Pig, The UMAP Journal 31(1) (2010), pp. 5–19.

Pour aller plus loin :

AfficherCacher