Il y a une semaine, le gouvernement publiait les derniers chiffres du chômage laissant place à une nouvelle vague de morosité dans les médias. Le timing semble bon pour rappeler que « sens critique » ne rime pas toujours avec « pessimisme ». Et à l’heure où les plus grandes chaines d’information ne jurent plus que par le « fact-checking », on serait bien tenté de s’agenouiller devant la sacro-sainte donnée brute, celle que l’on préfère priver d’analyse.
Heureusement, la vérité échappe souvent aux raisonnements les plus simplistes. Et alors qu’on nous assène de chiffres, passons en revue quelques exemples qui pourraient nous donner d’avantage à réfléchir la prochaine fois que la sentence de la décroissance sera prononcée.
Introduction à l’effet de Yule-Simpson
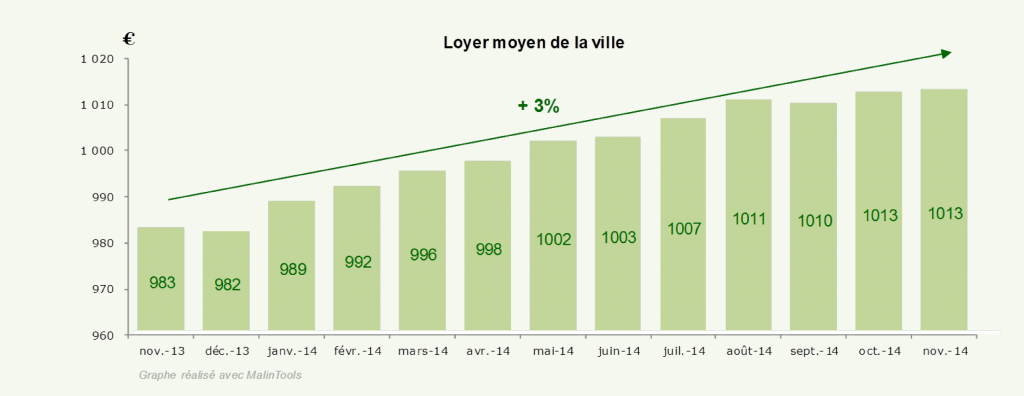
Mettons nous en situation, ce matin je lis mon journal, un café brûlant au bout des doigts, et j’apprends que le loyer moyen de ma ville a augmenté de +3% au cours des 12 derniers mois. Revêche, je me dis que le maire a encore loupé une occasion de tenir ses promesses.
Puis, curieux, j’avale d’un trait mon petit brun et décide de regarder dans quels arrondissements les loyers ont augmenté.
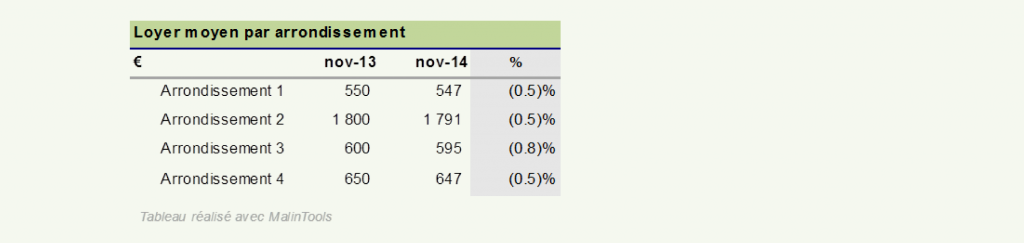
J’épluche alors les rapports de la mairie et constate que, loin d’avoir augmenté, les loyers moyens ont baissé dans tous les arrondissements de ma ville.
Dans chacun des 4 arrondissements, le loyer moyen a baissé entre 0.4 et 0.8%.
Je fais donc le constat insolite suivant: lorsque je regarde l’ensemble des locataires de ma ville, sur les 12 derniers mois, le loyer moyen a significativement augmenté mais lorsque je découpe ce même ensemble par arrondissement et que je regarde chaque arrondissement individuellement, tous les arrondissements ont vu leur loyer moyen diminuer.
En définitive, les mesures prises par le maire semblent finalement avoir été efficaces dans tous les arrondissements de la ville.
Voilà mon erreur admise et ma curiosité décuplée. En néophyte, je pourrais même penser que l’effet Yule-Simpson est un paradoxe ésotérique imprévisible.
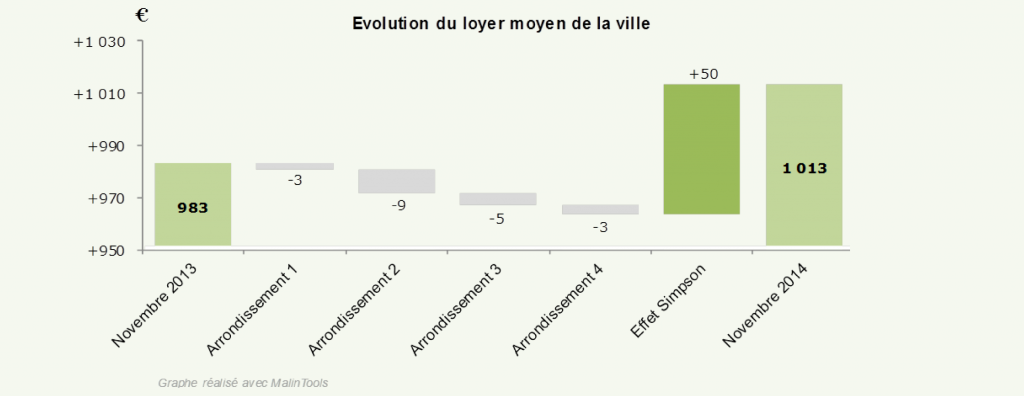
En réalité, l’effet Simpson répond à une logique implacable. Pour mieux comprendre, il faut s’attarder sur l’évolution de la répartition des locataires par arrondissement.
Un simple coup d’œil aux loyers moyens par arrondissement permet de remarquer que le 2ème arrondissement fait figure de quartier chic, les loyers y sont beaucoup plus élevés qu’ailleurs. Or durant les douze derniers mois, la part de locataires dans cet arrondissement a augmenté faisant subséquemment augmenter le loyer moyen de la ville et ce bien que le loyer moyen au sein même de cet arrondissement ait diminué.
Par conséquent, même si, pris individuellement, chaque arrondissement a vu son loyer moyen baisser, au global le loyer moyen de la ville a augmenté.
Le plus paradoxal dans cet exemple est que si je n’avais pas disposé de l’information par arrondissement, je me serais sans doute forgé une opinion négative de notre bon maire.
Application de Yule-Simpson aux derniers chiffres publiés par la DARES(1) :
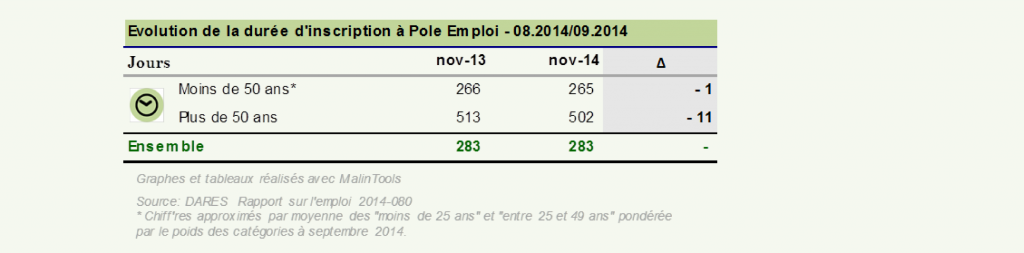
Intéressons-nous maintenant à l’impact du travail de l’agence pour l’emploi sur la durée d’inactivité des demandeurs d’emploi en France. Les chiffres publiés par la DARES semblent parler d’eux-mêmes, entre aout et septembre 2014, le nombre de demandeurs d’emploi de catégories A, B et C en France métropolitaine est passé de 5 078k à 5 128k et la durée d’inscription moyenne s’est maintenue à 283 jours.
Découpons maintenant cette population entre demandeurs d’emploi de moins de 50 ans et demandeurs de plus de 50 ans.
Surprise, une fois encore, la conclusion change et nous voilà bien forcés d’admettre que l’action de l’agence pour l’emploi a bien eu un effet positif sur ces deux sous-populations.
Ainsi étonne le paradoxe de Simpson. Mais ne vous y trompez pas, le phénomène n’est pas rare et apparait fréquemment dans les analyses de données statistiques. Les exemples historiques ne manquent d’ailleurs pas et je vous recommande ce très bon article du professeur Thomas C. Redman qui illustre un autre cas d’erreur d’interprétation propre au secteur du multimédia [le lien ici]
Mieux comprendre et anticiper le phénomène :
Le cœur de ce paradoxe repose sur (i) l’hétérogénéité de l’échantillon (les spécialistes parlent d’échantillon non randomisé) et sur (ii) l’existence d’un facteur de confusion, c’est-à-dire d’une propriété de l’échantillon (ici l’âge du demandeur d’emploi) possédant un fort coefficient de corrélation avec la variable observée (ici la durée d’inscription à pôle emploi). En réalité dans notre exemple, l’augmentation de la durée d’inactivité est expliquée par l’augmentation de la part de demandeurs d’emploi de plus de 50 ans sur la période.
Une fois encore, le plus troublant est que si nous n’avions pas disposé des données chiffrées par tranche d’âge, nous aurions pu finalement être tentés de conclure que, sur la période août-septembre :
- le nombre de demandeurs d’emploi a augmenté VRAI
- quel que soit l’âge d’un demandeur d’emploi, sa durée d’inscription moyenne d’inscription a également augmenté. FAUX
Nous sommes ici au plein cœur de la notion même de probabilité conditionnelle à l’origine de nombreux paradoxes (paradoxe des deux enfants, le paradoxe des deux enveloppes, le paradoxe des prisonniers,…).
Conclusion :
Beaucoup de gens confondent pessimisme et scepticisme. Le sens critique est une vertu qu’il est également bon d’employer quand le tableau est plus sombre. Quelques soient les situations, l’analyse est vitale et nécessite bien souvent plus de données que prévues.
Ainsi même lorsque la tendance est négative sur une population donnée (les français, les demandeurs d’emploi, …), il peut parfois suffire de découper cette population en sous-groupes cohérents pour faire apparaître une tendance plus positive sur toutes les sous-populations.
Ne rendons pas le tableau plus noir qu’il ne l’est, et lorsque toutes les données ne sont pas disponibles, restons prudents et ne sacrifions pas la confiance sur l’autel de la facilité.
(1)DARES : Direction de l’animation de la recherche, des études et des statistiques
References:
http://blogs.hbr.org/2014/10/when-it-comes-to-data-skepticism-matters
http://www.college-de-france.fr/site/stanislas-dehaene/course-2012-01-10-09h30.htm
http://sciencetonnante.wordpress.com/2013/04/29/le-paradoxe-de-simpson/
http://radio-weblogs.com/0101454/stories/2002/09/16/spamDetection.html
http://homepages.ulb.ac.be/~sgutt/probastatistique.pdf
Pour ceux qui veulent aller plus loin :
Afficher
Le paradoxe de Yule-Simpson s’intègre dans un cadre plus large : la théorie des probabilités conditionnelles, reposant notamment sur les travaux de Thomas Bayes. Cette théorie nous permet de distinguer deux probabilités bien distinctes d’occurrence d’un évènement. Prenons l’exemple de la probabilité d’obtenir un roi lorsque nous tirons une carte dans un jeu de 32 cartes. Nous distinguons alors :
- Sa probabilité à priori : elle caractérise la probabilité plausible d’occurrence de l’évènement avant d’en avoir observé les causes possibles. Ici, elle s’évalue à 0.125 (4/32).
- Ses probabilités à postériori : il s’agit des probabilités d’occurrence d’un évènement sachant qu’un autre évènement a été réalisé. Par exemple : la probabilité de tirer un roi, sachant que nous avons retiré du jeu de cartes toutes les cartes inférieures au valet.
On comprend facilement que l’on peut définir autant de probabilités à postériori que l’on veut pour un évènement donné.
Notons qu’il existe ainsi des méthodes d’évaluation de la probabilité à priori (plausibilité des hypothèses) à partir de la mesure de probabilités à postériori. C’est ce qu’on appelle l’inférence bayésienne et c’est notamment sur la base de ces méthodes que chaque jour vos mails sont classés ou non en SPAM. En lien ici, un article sur le sujet.
Dans l’exemple de la durée d’inscription à Pôle Emploi, nous n’effectuons pas de mesure de probabilité à priori. Ainsi pour chacun des mois d’août et de septembre, nous mesurons la durée moyenne d’inscription sachant que le nombre de demandeurs d’emploi de plus de 50 ans est de X%. Ce nombre X changeant entre les deux mois, nos moyennes ne sont pas comparables.
La clé est donc là, chaque analyse doit reposer sur une population d’individus comparables.
Une question doit maintenant vous brûler les lèvres et il s’agit sans doute du point le plus intéressant de ce problème.
Dans l’exemple de la durée d’inscription à Pole-Emploi, comment puis-je être sûr qu’il n’existe pas encore d’autres facteurs (département, sexe, tour de mollets, …) pouvant une nouvelle fois remettre en cause notre conclusion.
Pour répondre formellement à cette question, il nous faudrait :
- Disposer de ces données, or Pôle Emploi ne communique les durées d’inscription que par tranche d’âge.
- Établir que ces facteurs sont corrélés avec la durée d’inscription moyenne des demandeurs d’emploi
- Établir que cette corrélation accouche bien d’une causalité. Et là croyez-moi, le débat change de niveau…
En définitive, il ne nous reste que notre sens critique, et l’on pourrait bien légitimement penser que des analyses par sexe ou département de la durée d’inscription seraient des axes d’investigation intéressants à mener.
Une fois encore, une bonne politique de gestion repose avant tout sur la pertinence des indicateurs collectés. Quand ces indicateurs manquent, sans être des Pangloss, ne cédons pas à la morosité facile.