Le supposé Mari : « Je connais un jeu où je gagne toujours. »
L’inconnu : « Si vous ne pouvez pas perdre, ce n’est pas un jeu ! »
Le supposé Mari : « Je peux perdre, mais je gagne toujours. »
L’inconnu: « Essayons ! »
Ces répliques sont extraites du long-métrage d’Alain Resnais « l’année dernière à Marienbad ». Elles introduisent un scène marquante du film, où l’on voit deux hommes jouer à un jeu mystérieux où l’un des deux protagonistes semble battre perpétuellement son adversaire, impuissant, parties sur parties [extraits ici].
Les jeux avec une stratégie ‘gagnante à tous les coups’ semblent être légion, j’en ai pour exemple la dernière énigme que je vous ai soumise [pour rappel, c’est ici]. Toutefois, on peut facilement passer sa vie à les côtoyer sans savoir les reconnaître par avance.
Mais parce que l’anticipation n’est pas seulement l’apanage du mathématicien, à la fin de ce billet vous aurez les clés pour reconnaître simplement si le jeu auquel vous vous apprêtez à jouer possède une stratégie gagnante (qui d’ailleurs pourrait peut-être déjà être connue par votre adversaire…).
Introduction au théorème de Sprague-Grundy – les jeux de Nim
Dans la théorie des jeux, la théorie des jeux combinatoires fait figure de socle. Une théorie fondamentale sur laquelle toutes les autres ont pu s’appuyer (de la modélisation de la dissuasion nucléaire à la théorie économique des enchères).
Au sein de cette théorie féconde, un théorème se distingue par son originalité et sa nature tangible: le théorème de Sprague-Grundy.
Pour bien comprendre la portée de ce théorème, il faut d’abord comprendre le contexte. Nous sommes dans les années 30 et voilà presque 30ans que le mathématicien Charles Bouton a résolu un jeu très ancien appelé « jeux de Nim classique » ou depuis le film de Resnais « jeu de Marienbad ». Par « résoudre » j’entends qu’il a trouvé un algorithme permettant d’assurer une victoire certaine au joueur, pour peu que ce dernier se trouve dans une position dite ‘gagnante’.
Jeu de Nim classique ou jeux de Marienbad
Pour l’anecdote, le « jeu de Nim classique », popularisé par le film de Resnais, en a pris le nom mais initialement Marienbad est le nom d’une ville tchèque dans laquelle la belle Delphine Seyrig aurait eu une aventure avec l’un des personnages du film.
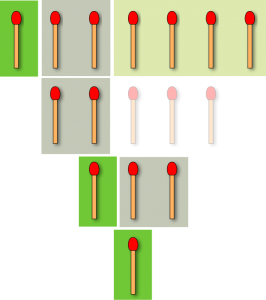
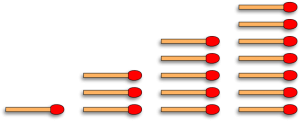
Dans le film, le jeu est simple. Sur une table sont disposées 4 rangées de 1,3,5 et 7 allumettes.
Généralisation et théorème de Sprague-Grundy
Chacun leur tour, les joueurs prennent le nombre d’allumettes qu’ils veulent, au moins une et dans une même rangée. Le joueur qui prend la dernière allumette a perdu (le film présente la version du jeu dite « misère »). A noté que dans la version « normale » du jeu, le joueur prenant la dernière allumette est considéré comme vainqueur.
Charles Bouton nous explique alors que dans ce jeu, les positions dans lesquelles peuvent se retrouver les tas d’allumettes se répartissent en deux groupes [les positions gagnantes et les positions perdantes].
Ainsi, selon la configuration au départ du jeu, l’un des joueurs aura une position gagnante, l’autre non. Si le joueur ayant hérité de la position gagnante effectue les bons coups, il gagnera à coup sûr et l’adversaire ne pourra que subir fatalement sa défaite. En revanche, au moindre mauvais coup, le joueur ayant hérité de la position gagnante pourra perdre son monopole, et son adversaire, s’il joue les bons coups, pourra reprendre le contrôle de la partie.
C’est d’ailleurs bien dans cette notion de positions gagnantes et perdantes que la réplique « je peux perdre mais je gagne toujours » prend tout son sens. L’homme ne démarrant pas systématiquement dans une position gagnante: « il peut perdre », toutefois son adversaire ne connaissant pas la stratégie gagnante (que je vous présente plus bas), il finira toujours par se retrouver dans une position gagnante et donc « gagne toujours ».
En 1930, on pouvait donc naturellement penser que Bouton avait fait le job. C’était sans compter sur deux mathématiciens: Roland Sprague (allemand) et Patrick Grundy (britannique) qui , respectivement en 1935 et 1939 vont démontrer indépendamment (oui à cette époque, les échanges scientifiques entre les deux pays étaient un peu dégradés) que la théorie de Bouton peut se généraliser à l’ensemble des jeux impartiaux.
Reconnaître un jeu avec une stratégie gagnante – les jeux impartiaux
Maintenant, retenez donc ce qui va suivre car tout jeu impartial possède une stratégie gagnante à coup sûr dès lors que le joueur se retrouve dans une position gagnante.
Un jeu impartial est définit comme suit:
- C’est un jeu opposant deux joueurs, jouant alternativement.
- A tout moment du jeu, les deux joueurs ont une connaissance parfaite de l’état de ce dernier. On dit que le jeu est à information complète (exit donc la bataille ou le poker).
- Il n’y a aucune intervention du hasard au cours du jeu.
- Les coups des joueurs permettent de faire passer le jeu d’une position à une autre selon des règles définies.
- A partir d’une position donnée, les positions accessibles par un joueur sont appelées ses options. Les options disponibles sont toujours les mêmes pour les deux joueurs (exit donc les échecs ou les dames qui appartiennent à la famille des ‘jeux partisans’)
- Les règles doivent être définies de telle sorte que toute partie se termine en un nombre fini de coups et ne doit pas pouvoir laisser place à un match nul (exit donc le morpion).
- La partie se termine lorsqu’un joueur ne peut plus jouer (« version normale »)
Dès lors que les conditions ci-dessus sont vérifiées, vous pouvez affirmer qu’il existe une stratégie « gagnante à tous les coups » pour ce jeu. Et j’ai envie de vous dire, si vous vous arrêtez là, vous avez déjà assimilé l’une des notions les plus importantes de ce billet.
Trouver la stratégie gagnante – Application au jeu de Marienbad
Si connaitre l’existence d’une stratégie gagnante semble être relativement facile, déterminer cette stratégie peut parfois s’avérer plus sport.
Ci-dessous, nous allons voir la méthode générale développée par Sprague et Grundy et appliquée au cas du jeu de Marienbad. Il s’agit de la méthode théorique généralisable à tout jeu impartial mais je vous expliquerai ensuite pragmatiquement comment faire le travail de tête lors d’une partie.
1. Méthode théorique générale – les moins courageux pourront esquiver cette partie
Pour simplifier un peu la chose, nous n’allons pas jouer à la version « misère » comme dans le film d’Alain Resnais, mais à la version « normale » (ie que le joueur prenant la dernière allumette a gagné).
Etape 1 : Trouver les nimbers
La notion de nimber, juste contraction des mots ‘Nim’ et ‘number’, est un pilier de la théorie des jeux combinatoire. Un nimber désigne un ‘jeu de Nim à un seul tas’ (par opposition au 4 tas d’allumettes décrits plus haut) mais par extension on appelle également nimber, un nombre entier caractéristique d’une position donnée pour un ‘jeu de Nim à un tas’. [Remarque; le nimber est aussi parfois appelé ‘nombre de Grundy’ ou ‘nimbre’ pour les anglophobes].
Dans le cas du jeu de Marienbad du film de Resnais, il y a quatre tas d’allumettes donc quatre nimbers. Reste à voir comment calculer ces nimbers.
Le nimber d’un tas se définit alors comme ce qui suit:
- Le nimber de la position finale vaut 0
- Le nimber d’une position donnée est définit comme le plus petit entier naturel (ie positif ou nul) n’apparaissant pas dans la liste des nimbers des positions pouvant suivre immédiatement cette position.
Alors comme ça… ça peut sonner un peu cabalistique mais avec des exemples tout est plus clair:
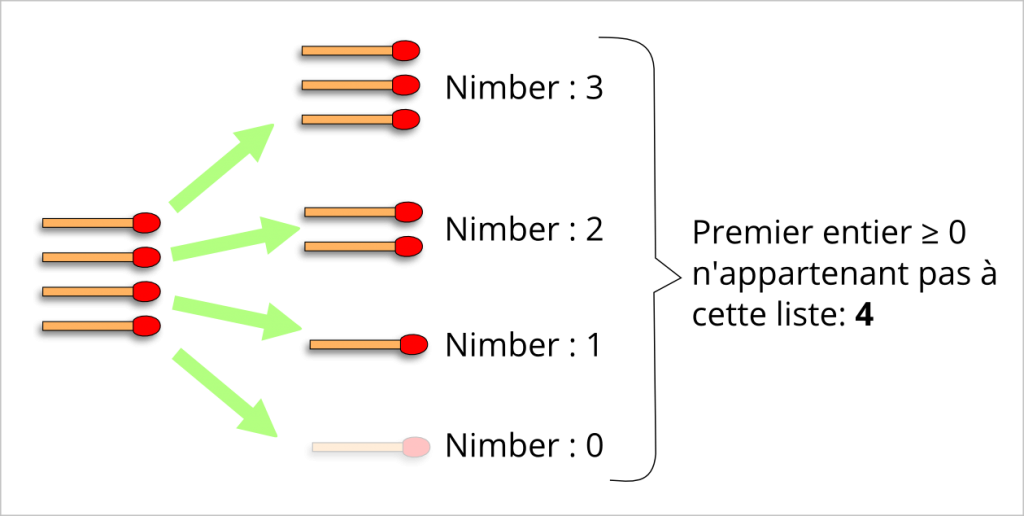
Pour un tas de 0 allumette: le nimber est 0 (cf définition).
Pour un tas de 1 allumette: le nimber est 1. Lorsqu’il ne reste qu’une allumette, je n’ai pas le choix : je vais enlever une allumette et la position suivante sera un tas de 0 allumette. La liste des nimbers des positions suivantes est donc {0}.
Le plus petit entier positif n’appartenant pas à la liste {0}, c’est bien 1.
Pour un tas de 2 allumettes: le nimber est 2. Lorsqu’il reste deux allumettes, je peux soit choisir d’en retirer une, soit deux : la positions suivantes possibles sont « un tas de 0 allumette » ou « un tas de 1 allumette ». La liste des nimbers des positions suivantes possibles est donc {0,1}.
Le plus petit entier positif n’appartenant pas à la liste {0,1}, c’est bien 2.
Dans le cas du jeu de Marienbad, les nimbers correspondent donc aux nombres d’allumettes de chaque tas (facile!)
Remarque: Imaginons que nous soyons dans une émission de télévision grand publique et que je porte un masque à tête de tigre (grrrr). J’aurais alors pu rajouter la règle « chaque joueur ne peut enlever que 1,2 ou 3 allumettes » dans ce cas:
Pour les tas de 0,1,2 et 3 allumettes, tout marche pareil, mais c’est après que les nimbers changent un peu.
Pour un tas de 4 allumettes, la position 0 allumette ne peut pas être atteinte (je ne peux retirer que 3 allumettes au maximum). La liste des nimbers des positions suivantes sera donc {1,2,3} et le plus petit entier naturel n’appartenant pas à cette liste c’est 0.
Pour un tas de 5 allumettes, le nimber est 1
6 allumettes: le nimber est 2 …
et ainsi de suite.
Pour un tas de n allumettes, le nimber est donc définit comme le reste de la division euclidienne du nombre d’allumettes du tas par 4.
Etape 2 : Chercher à annuler la somme de Nim des nimbers
Et maintenant on fait quoi avec nos nimbers?
Et c’est là que Sprague et Grundy interviennent. En effet, le théorème de Sprague-Grundy nous explique que tout jeu impartial peut être transformé en un « jeu de Nim à un tas » équivalent possédant un nimber propre à chacune de ses positions. Pour le cas du jeu de Marienbad (Bouton l’avait déjà démontré), le nimber global du jeu peut s’obtenir en faisant la somme de Nim des différents nimbers.
Une fois cet unique nimber obtenu et propre à chaque position du jeu.
La stratégie gagnante (pour la version ‘normale’) consistera toujours à agir sur le jeu de manière à annuler ce nimber global.
Donc comme nous l’avons dit, pour le jeu de Marienbad, ce nimber s’obtient en faisant la somme de Nim des nimbers des différents tas.
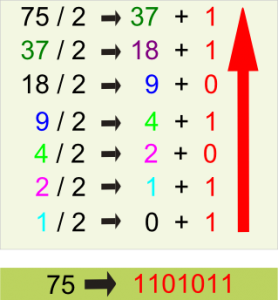
Pour effectuer cette opération un peu spéciale, il faut commencer par passer tous nos nimbers en binaire.
Alors, pour rappel, écrire un nombre en binaire c’est décomposer ce nombre en une somme de puissances de 2.
L’astuce pour convertir facilement un nombre décimale en binaire consiste à le diviser plusieurs fois par 2 et regarder le reste Euclidien de chacune de ces divisions (cf figure 3, ci-contre).
Une fois nos quatre nimbers passés en binaire, il faut les sommer un à un avec les règles suivantes (les informaticiens reconnaîtront une somme XOR):
- 0+0=0
- 1+1=0
- 1+0=0+1=1
Dans notre cas précis, notre somme est égale à 000
Et comme l’objectif poursuivit par une stratégie gagnante est de toujours faire passer cette somme de Nim à 000, on constate donc que la position initiale est une position perdante. En effet, puisque la somme de Nim est déjà égale à 0, toute action de jeu la fera varier vers un résultat différent de 000 (c’est pas moi qui le dit, c’est Bouton!).
Mise en application:
Imaginons que votre adversaire joue en premier, vous êtes donc dans une position gagnante…
Si vous vous appliquez, votre adversaire n’a aucune chance de gagner. Votre adversaire prend deux allumettes dans la pile de 7 allumettes. La nouvelle configuration est donc : 4 rangées de 1,2,5 et 5 allumettes.
La somme de Nim est alors de 010.
Il vous faut donc refaire passer cette somme à 000. Pour cela vous pouvez retirez deux allumettes au tas de 3 allumettes.
2. Méthode pratique appliquée au jeu de Marienbad
Et si je vous disais que nous n’êtes pas obligé de faire toutes les conversions décimales-binaires décrites dans la méthode théorique et que, comme Néo devant une cascade de nombres tout droit sortis de la Matrice, vous pourriez bien voir et travailler directement en binaire sans vous en rendre compte.
Pour cela, pour chaque rangée d’allumettes, essayez de regrouper mentalement vos allumettes par groupe de 4, 2 et 1 allumette en essayant de n’avoir qu’un groupe de chaque maximum par rangée. Pour cela, essayez d’abord de construire vos groupes de 4, puis vos groupes de 2 et enfin seulement vos groupes de 1 avec les allumettes restantes.
 |
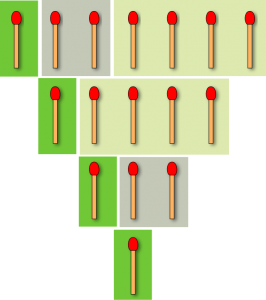| figure 4 – application pratique de Sprague-Grundy – Etape 1 |
La stratégie gagnante consiste alors à toujours essayer de revenir dans une situation où chaque regroupement est présent en nombre pair (0,2 ou 4).
Maintenant, l’action de votre adversaire va perturber ces groupes. Imaginons qu’il enlève 3 allumettes à la deuxième ligne.
|
|
| figure 4 – application pratique de Sprague-Grundy – Etape 2 |
Les regroupements ne sont plus présents en nombres pairs. [3 regroupements de 1 allumette, 3 regroupements de 2 allumettes et 1 regroupement de 4 allumettes]. Vous allez devoir remédier à ça.
- Impossible de recréer un groupe de 4 allumettes, vous allez donc devoir casser ce groupement en première ligne. Il faudra donc enlever au moins 4 allumettes en première ligne.
- Puis en ne touchant qu’à la premier ligne, vous allez devoir créer ou enlever un groupement de 1 allumette et un 1 groupement de deux allumettes. Pour cela il vous faudra enlever 3 allumettes supplémentaires dans la première rangée.
 |
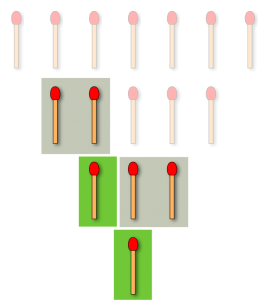| figure 4 – application pratique de Sprague-Grundy – Etape 3 |
Voilà, tout ça sans une conversion en nombre binaire!
Conclusion – une histoire de symétrie
Au final, lorsqu’on se trouve sur une position gagnante, la stratégie gagnante d’un jeu impartial consiste toujours à systématiquement annuler l’action qu’a effectuée l’adversaire (pour se retrouver de nouveau sur une somme de Nim nulle, pour ceux qui ont lu la partie théorique). Dès lors, quoi de plus normal, lorsqu’une symétrie physique se dégage sur le plateau de jeu, d’imiter systématiquement son adversaire en reproduisant symétriquement ses actions. C’est le cas pour un jeu de Marienbad avec, par exemple, 4 piles de 7 allumettes chacune, mais c’est également le cas pour le jeu des pièces décrit dans l’énigme du week-end dernier [ici].
Vous voilà maintenant l’heureux receleur de la théorie de Sprague-Grundy. Théorie qui, j’en suis sûr, vous conférera un avantage notoire dans votre labeur quotidien. En attendant, vous pouvez dors et déjà aller jeter un œil à ces exemples de jeux impartiaux: jeu des bâtonnets, quart de singe, jeu de Wythoff, jeu de Cram, le jeu des sprouts, le chomp ou jeu du chocolat empoisonné, …
Références:
Traitant du sujet:
https://interstices.info/jcms/i_61780/strategies-magiques-au-pays-de-nim
http://web.mit.edu/sp.268/www/nim.pdf
https://math.berkeley.edu/~liangrc/ttc/Report.pdf
http://eljjdx.canalblog.com/archives/2009/08/01/14595654.html
Pour celles et ceux qui aimeraient trouver la fonction de Grundy permettant d’obtenir le nimber de la position initiale du jeu des pièces, pas facile mais une piste ci-dessous:
http://mathworld.wolfram.com/CirclePacking.html