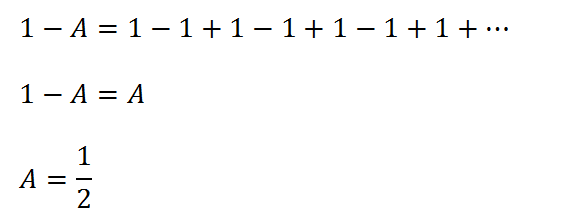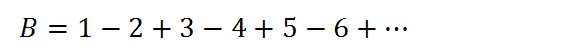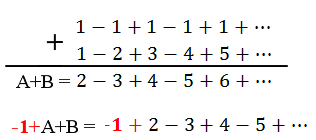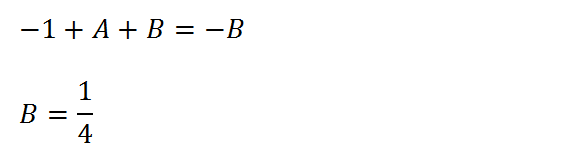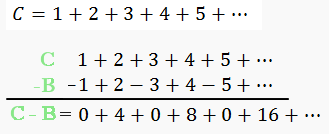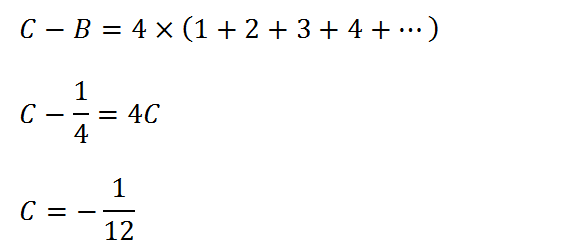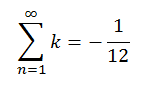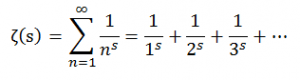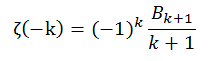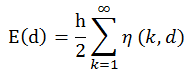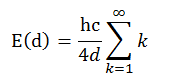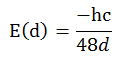Vous avez un peu de temps devant vous? Faisons donc ensemble un petit jeu d’esprit:
A quoi pourrait être égale la somme des nombres entiers positifs:
1+2+3+4+5+6+7+… comme ça jusqu’à l’infini…
Et badaboum, la réponse est unanime : l’infini!
(Bon préparez vous à lever l’index et à afficher votre plus beau rictus)
Si je vous disais maintenant que 1+2+3+4+5+… = -1/12.
De quoi qu’on cause?
Ne vous y trompez pas, il ne s’agit pas d’une nouvelle arnaque où je planque discrètement une division par 0 dans mes calculs pour vous prouver que 1=0. Ce résultat est admis par la communauté scientifique et je vous invite à parcourir les références citées en bas de page pour vous convaincre que si quelque chose cloche encore à la fin de ce billet c’est que vous ne regardez probablement pas le problème avec le bon angle.
En fait, à bien y regarder, l’idée de dire que tous les infinis ne se « valent » pas n’est pas récente.
Dès le début du XXème siècle, un mathématicien allemand du nom de Georg Cantor vient nous expliquer que les nombres réels (1, 2.335597, π ,…) sont plus « nombreux » que les nombres entiers.
L’idée à de quoi troubler… ces deux quantités sont infinies et l’infini c’est l’infini… non?
En fait, il existe un exemple qui illustre assez bien ce qu’a montré Cantor : le paradoxe de l’hôtel de Hilbert. Vous pouvez retrouver ce paradoxe amusant dans un autre de mes billets : L’hôtel de Hilbert – Y a -t-il quelque chose de plus grand que l’infini ?
Voyons maintenant comment l’on peut montrer simplement que la somme de tous les nombres entiers peut être égale à -1/12.
Explication (notions requises: addition et soustraction)
Etape 1 : regardons ensemble la somme 1-1+1-1+1-1+… admettons que son résultat puisse être défini et appelons le A:
Si on regarde à quoi ressemble 1-A, on s’aperçoit que l’on retrouve exactement la même série de 1 et -1 que ci-dessus. Les deux membres sont donc égaux et l’on peut en déduire A facilement.
Etape 2 : maintenant regardons la somme 1-2+3-4+… une fois encore admettons l’existence d’un résultat que l’on appellera B.
Toujours dans une infinie curiosité, regardons à quoi pourrait ressembler A+B puis -1+A+B
Une fois encore, on reconnait la série des termes de B avec toutefois un signe opposé. On a donc l’égalité suivante qui nous permet également de définir B (maintenant que l’on connait A).
Etape 3 : Enfin regardons la somme qui nous intéresse 1+2+3+4+… et appelons son résultat C.
Plus précisément regardons la différence des résultats C-B.
En faisant un peu appel à nos souvenirs de primaire et à l’angoisse du tableau noir, on reconnait une série qui ressemble fort à la table du 4. On peut donc factoriser l’expression pour faire apparaître le terme 4xC, puis en déduire C (maintenant que l’on connait B).
Nous y voilà, l’égalité 1+2+3+4+5+…=-1/12
Pour celles et ceux qui ont levé le doigt dès le début de la démonstration, je vous donne rendez-vous tout en bas du billet dans le chapitre ‘pour aller plus loin’.
Bon ok, c’est quoi le truc?
En fait, derrière ce résultat paradoxal se cachent les fondements de ce qui est aujourd’hui considéré comme le plus grand problème mathématique jamais démontré: l’hypothèse de Riemann (2).
David Hilbert, une belle pointure en mathématiques, aurait à ce titre confié « si je devais m’endormir pendant 1000 ans, la première chose que je demanderai à mon réveil serait ‘l’hypothèse de Riemann a -t-elle été démontrée?' ».
Même si je pense qu’Hilbert en pareilles circonstances aurait d’abord demandé les toilettes, il est vrai que ce problème a fasciné des générations entières de mathématiciens, et pour cause, il flirte avec la partie la plus démoniaque des mathématiques: les séries divergentes (Mouhahaha…).
Le problème intellectuel lié à cette somme, c’est que l’on a du mal à considérer la somme des nombres entiers positifs comme un objet nouveau et totalement différent d’une somme gigantesque (mais finie) de nombres.
Pourtant le problème est bien là! Imaginons que je prenne la somme des entiers naturels allant de 1 jusqu’à un gogolplex(1), (un gogolplex c’est vraiment énorme, je vous invite à aller jeter un coup d’oeil à la note de fin de page). Et bien même cette somme, aussi immense soit-elle, n’est pas du tout comparable à la somme des entiers positifs. Ces deux sommes sont de natures complètement différentes, cela revient à comparer un choux avec une mangouste… et c’est là dessus que repose le côté paradoxal du résultat -1/12.
Je m’explique, depuis votre tendre enfance on vous a défini l’addition comme l’opérateur vous permettant de calculer les bonbons que vous aurez quand Jacques et Paul vous auront filé les leurs. Cette définition avait l’avantage de combiner l’enseignement des mathématiques et de l’altruisme, mais a le fâcheux inconvénient de très mal s’appliquer à des objets mathématiques un peu particuliers: les sommes infinies de nombres.
En d’autres termes, le signe « + » que j’ai utilisé plus haut n’est pas celui que vous connaissez, ou plus exactement il est plus que ça!
On y vient.
Puisque je n’arrive manifestement pas à définir un résultat lorsque le nombre de termes de mon addition est infini, je vais devoir définir un opérateur qui me le permettra mais qui correspondra aussi exactement à mon opération « + » (celle de Jacques et Paul) lorsque le nombre de termes de mon addition est fini.
C’est ce que nous avons tacitement fait dans la démonstration ci-dessus et ce qui est fait plus explicitement dans le chapitre ‘pour aller plus loin’.
Ok mais ça veut dire quoi ce résultat, concrètement?
A ce moment précis, vous vous dites surement « super, encore un délire de mathématicien ».
Pas faux, mais comme bien souvent dans l’histoire, les mathématiciens fabriquent des objets théoriques puis les physiciens piochent dans ces boîtes à outils pour résoudre des problèmes bien réels.
Et le fait est, qu’ici encore, la physique a trouvé des applications effectives au résultat évoqué plus haut.
Pour ceux qui n’en aurait jamais entendu parler, l’effet Casimir prévoit que deux plaques conductrices placées dans le vide s’attirent mutuellement.
Cette force attractive, expliquée par les fluctuations quantiques du vide, a tenté d’être calculée par ce bon Casimir.
Sans rentrer dans les détails, la difficulté admise de ce calcul réside dans le fait que si vous admettez que le vide possède une énergie, dès lors vous vous retrouvez avec des sommes infinies.
Vous pouvez finalement vous extraire de cette passe difficile avec le résultat
Mais comble de l’ironie mathématique (je viens de l’inventer celle là), en 1997 le chercheur Steve Lamoreaux publia dans Nature les résultats de son expérience qui venaient valider les calculs de Casimir effectués 50 ans plus tôt.
Pour plus de détail sur ces calculs, allez jeter un oeil à la partie ‘pour aller plus loin’
Conclusion – s’extraire du système
En fait, vous ressentez probablement aujourd’hui la même chose que moi le jour où j’ai appris au lycée qu’il existait une solution à l’équation:alors qu’on m’avait bien dit jusqu’alors que tous les nombres carrés étaient positifs!!!
Le sentiment d’incompréhension et de vertige lorsque vous êtes dans une chambre, qu’on vous ouvre une porte (pour moi celle des nombres complexes, pour vous celle des opérations sur les séries divergentes) et que tout d’un coup, par le biais d’un passage dans cette nouvelle pièce mystérieuse vous réalisez que vous pouvez accéder à d’autres coins de votre chambre qui vous étaient jusqu’alors inaccessibles sinon inconnus.
Ce point est joliment illustré dans le roman FlatLand de Edwin Abbott Abbott.
L’histoire, qui se déroule dans un monde plat (ie en 2 dimensions), nous raconte comment l’un de ses habitants (un carré), voyant un jour apparaître une sphère, va tenter de convaincre ses congénères de l’existence d’une troisième dimension spatiale.
Le roman est écrit à la première personne et l’on suit le point de vue du carré. On nous explique notamment que dans ce monde plan, où seuls deux dimensions existent, la lumière est présente partout même à l’intérieur des habitations pourtant complètement fermées. Les habitants ne comprennent pas d’où vient cette lumière car elle vient d’en haut et donc d’une dimension qu’ils ne peuvent pas percevoir. Je trouve amusant le parallèle que l’on peut tracer avec ce que l’on appelle aujourd’hui l’énergie sombre (ou énergie noire) qui est une forme d’énergie emplissant uniformément tout l’univers et dont l’origine reste encore mystérieuse (un peu comme la lumière baignant uniformément FlatLand).
Alors je sais, comme ça, ça sonne un peu ésotérique, mais c’est super court et ça se lit bien.
Alors si maintenant, comme moi, vous vous sentez animé d’une foi indéfectible en l’ignorance humaine, n’oubliez pas ce que ce bon Albert disait: « ce qui est incompréhensible, c’est que le monde soit compréhensible ». [« Comment je vois le monde » A.Einstein 1934]
(1) un gogolplex: c’est 10^gogol… et un gogol c’est 10^100.
On estime que le nombre de particules dans l’univers est 10^20 fois inférieur à un gogol.
Ainsi, si un gogol peut s’écrire comme un 1 suivi de 100 zéros derrière.
Le gogolplex, quant à lui, ne peut tout simplement pas s’écrire!! en effet même si j’arrivais à écrire des zéros de la taille d’une particule physique, il me faudrait un peu plus de 100 milliards de milliards d’univers pour pouvoir tous les écrire. De quoi donner le vertige, non?
(2) L’hypothèse de Riemann définit la fonction ζ (prononcé zêta) comme :
Avec s : un nombre appartenant à l’ensemble des nombres complexes privé de 1 (pour la définition de la fonction sur l’ensemble des complexes à partie réelle négative voir le chapitre ‘pour aller plus loin’).
Remarquons que notre égalité peut alors s’écrire ζ(−1)=-1/12, on remplace dans la fonction ci-dessus les s par -1.
L’hypothèse de Riemann conjecture alors que cette fonction s’annule uniquement pour :
(i) des nombres réels négatifs paires (eh oui ζ(−2)=0!); et
(ii) pour des nombres complexes avec une partie réelle égale à 1/2. Si l’on se figure un nombre complexe comme un point à deux coordonnées sur un plan, cela veut dire qu’à droite de l’axe des ordonnées, la fonction zêta ne s’annule que sur une droite verticale d’équation x=1/2.
C’est cette deuxième partie (ii) que les mathématiciens n’ont toujours pas réussi à démontrer.
Et si les scientifiques s’acharnent à démontrer ce problème, c’est que sa résolution permettra de résoudre bien d’autres problèmes actuellement ouverts en mathématiques ou en physique (répartition des états d’énergie d’un atome, répartition aléatoire des nombres premiers,…).
Anecdotiquement, l’hypothèse de Riemann nous a déjà démontré que l’on est pas obligé de savoir de quoi on parle pour publier dans un grand quotidien. En effet, en 2004, un journaliste du Guardian nous expliquait que la démonstration de la conjecture de Riemann nous guiderait vers un cataclysme Internet [ici]. L’idée, reprise par d’autre depuis, fait référence aux modes de cryptage reposant sur la difficile factorisation des nombres premiers… Or l’hypothèse de Riemann, si elle était démontrée, expliquerait justement que les nombres premiers sont répartis aléatoirement au sein des entiers… Je ne vois pas vraiment comment le fait de savoir que les nombres premiers sont répartis aléatoirement pourra aider un hacker à factoriser un nombre premier.
Références:
Autres articles sur le sujet:
1.Article vraiment bon et accessible:
https://sciencetonnante.wordpress.com/2014/01/20/le-scandale-des-series-divergentes/
2.Une petite vidéo du génial Mickaël Launay:
https://www.youtube.com/watch?v=xqTWRtNDO3U
Fonctions zêta:
3.Prolongement analytique de zêta sur l’ensemble des complexes privé de 1:
http://fr.wikipedia.org/wiki/Fonction_z%C3%AAta_de_Riemann#Extension_.C3.A0_.E2.84.82-.7B1.7D
4.Un traitement plus arithmétique de la fonction zêta:
http://www.math.polytechnique.fr/xups/xups02-02.pdf
5.Un article plus général sur les travaux de Riemann et son prédécesseur Euler:
https://jfresan.files.wordpress.com/2011/04/lecture-de-riemann.pdf
Nombre de Bernouilli:
6.http://fr.wikipedia.org/wiki/Nombre_de_Bernoulli
Effet Casimir:
7.http://www.scholarpedia.org/article/Casimir_Force
8.http://www.larecherche.fr/savoirs/physique/force-qui-vient-du-vide-01-06-2004-88969
Pour aller plus loin (déconseillé à ceux qui n’aiment pas les formules)
Afficher
Une démonstration un peu plus rigoureuse
Notions requises: ensemble de définition d’une fonction, nombres complexes
La démonstration plus haute, inspirée des calculs d’Euler, a la fâcheuse tendance d’utiliser des objets non définis. Eh oui, je vous ai bien demandé d’admettre que que la somme 1-1+1-1+1… avait un résultat…
Pour faire les choses un peu plus sérieusement, il nous faut définir une extension à la fonction ζ (prononcé zêta) ci-dessous:
A première vue, la fonction ci-dessus n’est définie que pour les complexes à partie réelle >1.
L’idée est donc de trouver une fonction définie pour tous nombres complexes (à l’exception de 1), qui coïncide avec zêta pour les valeurs où elle est déjà définie. Cette nouvelle fonction sera ce qu’on appelle le prolongement analytique de zêta (ou prolongement holomorphe pour ceux qui préfèrent les racines grecs aux racines latines).
En fait, il existe plusieurs démonstrations possibles pour montrer l’existence de ce prolongement analytique.
Ces démonstrations utilisent toutes des représentations différentes de la fonction ζ et vous pouvez retrouver les principales ici.
Avec très peu d’effort, on peut même démontrer que ce prolongement analytique est unique.
Ainsi, je peux choisir au hasard l’une des extensions formalisées par les démonstrations données dans le lien ci-dessus. Par exemple:
avec Bk+1, le k+1ème nombre de Bernouilli (à ne pas confondre avec les polynômes de Bernouilli).
Enfin, il ne me reste plus qu’à calculer mon résultat pour k=1.
Ma table des nombres de Bernouilli m’indique B2 =1/6, je retrouve donc bien ma valeur -1/12.
Ainsi j’obtiens bien ζ(−1)=-1/12
Calcul de la force de Casimir
En très vulgarisé:
La fluctuation quantique c’est le changement temporaire du niveau d’énergie à un point donné de l’espace. Son plus faible état d’énergie est appelé énergie du point zéro (que l’on appelle aussi parfois ‘énergie du vide’). En gros, c’est l’énergie qui existe par défaut dans l’univers (un genre d’offset).
Si l’on admet que l’on se place dans le cadre d’oscillateurs harmoniques quantiques (c’est à dire que tous les champs varient sous la forme de jolis sinus), nous pouvons évaluer cette énergie à :
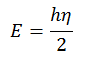(résultat admis : résultante des équations de Schrodinger)
Avec h une constante appelée constante de Planck et η la fréquence de fluctuation de nos photons.
Dans le case du vide, il faut donc sommer tous les différents modes de champs possible (toutes les fréquences possibles).
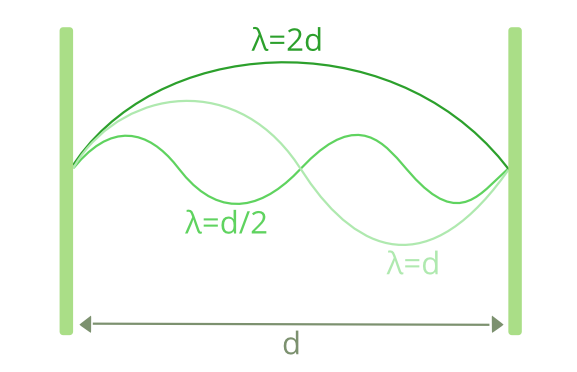
Dans le cas d’un espace entre deux plaques, les fréquences possibles sont uniquement celles dont la longueur d’onde divise exactement le double de la distance entre les deux plaques. (ce point, que je vous demande d’admettre, est la conséquence d’une condition aux limites imposée par le fait que le champ électrique des photons doit être nul au niveau de la plaque) [Cf figure ci-dessous].
Au final, nous avons donc:
avec E l’énergie par unité de surface, d: la distance entre les deux plaques, η la fréquence d’oscillation de nos photons aussi égale à c/λ avec
c: la vitesse de la lumière et
λ: la longueur d’onde de la forme = 2d/k (cf ce que l’on a vu plus haut)
Finalement nous avons la somme:
En utilisant le résultat plus haut de -1/12. On obtient finalement:
Il ne reste plus qu’à dériver par rapport à d pour obtenir notre force de d’attraction par unité de surface. C’est en effet bien le signe négatif du -1/12 qui confère la propriété d’attractivité à la force.
Si vous voulez un peu plus de détails, je vous recommande cet article [ici] ou en plus vulgarisé cet article [ici].
Dans le premier lien, l’auteur utilise une approximation physique dans son calcul mais arrive finalement bien au même résultat (en remplaçant la constante de Planck par sa forme normalisée).