En réponse à la question pertinente d’un lecteur curieux, je me permets de déposer un complément au billet Le jour où l’infini a été évalué à -1/12. Si vous ne l’avez pas lu, je vous conseille d’abord d’aller y jeter un coup d’oeil [c’est par ici].
Ce complément aborde des considérations mathématiques et se veut donc un peu moins vulgarisé que les autres. 

Etape 1: La question et sa réponse

Question : j’ai suivi ta méthode permettant d’obtenir 1-1+1-1+1…=1/2. Je l’ai appliqué à la somme :
1+1+1+1+…=J
J’obtiens alors 1+J=J, soit 1=0.
Je ne comprends ce résultat. N’invalide-t-il pas ta méthode de démonstration ?

Réponse : c’est une excellente remarque qui met en lumière les raccourcis de la première démonstration. Toutefois, ce résultat n’invalide ni le résultat ni sa démonstration mais exige quelques explications.
Si l’on avait voulu faire les choses un peu plus sérieusement, on aurait d’abord expliqué ce qu’il faut à un « + » pour qu’il soit considéré comme une vraie méthode de sommation. Traditionnellement (je reviens dessus un peu plus tard), une méthode de sommation respecte trois propriétés :

• La linéarité : Cela veut dire que si  j’ai une série de termes An dont la somme vaut A (respectivement Bn dont la somme vaut B) alors la somme des termes An+λBn vaut A+λB.
• La régularité : c’est le fait que, pour toutes les sommes finies de nombres, la méthode de sommation coïncide avec la méthode usuelle de sommation (le «+» que l’on utilise depuis tout petit) (j’en parle dans mon premier billet).
• La stabilité : c’est le fait que l’on puisse toujours extraire un nombre fini de termes en début de série, de sorte que  ΣAn= (A0+A1+A2 + …+Ak) + ΣAn+k

En fait, dans la première démonstration de mon précédent billet, je fais une hypothèse implicite qui est :
« Supposons qu’il existe une méthode de sommation stable, linéaire et régulière permettant de sommer la série série (1,-1, 1, -1,…) alors… »
Puis j’utilise ces trois propriétés  pour obtenir finalement … A=1/2.
Cette hypothèse est valable pour la série (1,-1, 1, -1, 1,…) parce que d’autres l’ont démontrée avant moi. Cette série s’appelle d’ailleurs la série de Grandi et voici un article détaillé [ici] Du coup, lorsque vous obtenez 0=1 en utilisant cette démonstration pour la série 1+1+1+1+… vous démontrez (par l’absurde) qu’il n’existe pas de méthode de sommation stable, linéaire et régulière permettant de sommer la série (1,1,1,1,…).
D’ailleurs, en guise de remarque, si vous regardez les méthodes de sommation d’Abel, elles ne sont définies que pour des suites de réels positifs strictement croissantes tendant vers l’infini.
[Article ici]

Etape 2: Discussion sur les propriétés de la méthode de sommation permettant d’obtenir 1+2+3+…= -1/12

Un peu plus haut, je vous ai dit que les méthodes de sommation respectent traditionnellement les propriétés de régularité, linéarité et stabilité.
En fait, ces trois propriétés sont très lourdes à respecter et les scientifiques choisissent parfois de s’affranchir de certaines d’entre elles.
Ainsi certaines méthodes importantes, telles que la sommation de Borel ne sont pas stables…
De même, en analyse complexe, il arrive parfois que l’on abandonne les propriétés de régularité et de linéarité pour aboutir à des méthodes d’approximation plus puissantes, c’est notamment le cas de la méthode de l’approximant de Padé.
Et je ne vais pas vous le cacher plus longtemps, le « + » de notre somme 1+2+3+4+…=-1/12 ne respecte pas l’ensemble des trois propriétés énoncées plus haut.
Une façon simple de s’en convaincre est de regarder ce que vaut le prolongement analytique de Zêta en 0. Pour rappel, Zêta est défini comme: 

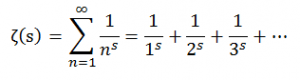Pour s=0, il s’agit de notre somme 1+1+1+1+…

Et bien, alors que nous avions démontré ensemble plus haut qu’il n’existait pas de méthode de sommation linéaire, régulière et stable pour la série (1,1,1,1,…), le prolongement analytique de Zêta est, quant à lui, bien défini en 0 et vaut -1/2.
Et oui, 1+1+1+1+… = -1/2 (l’article wikipedia sur ce sujet : [ici])
En fait, la méthode de sommation utilisée pour trouver notre résultat -1/12 ne respecte pas au moins une des propriétés de linéarité, régularité et stabilité.

En réalité, l’on peut démontrer facilement que s’il existe une méthode de sommation applicable à la série (1, 2, 3, 4,…), elle est alors soit linéaire, soit stable (mais pas les deux).
En guise d’aveu, la méthode de régularisation de la fonction zêta évaluée en s=-1 (démonstration illustrée dans la section ‘pour aller plus loin’ de mon précédent billet) présente une méthode de sommation stable mais non linéaire… mais, disons le nous, cela n’enlève rien à son côté déroutant.